数 近似値 近似式 数学のコツ
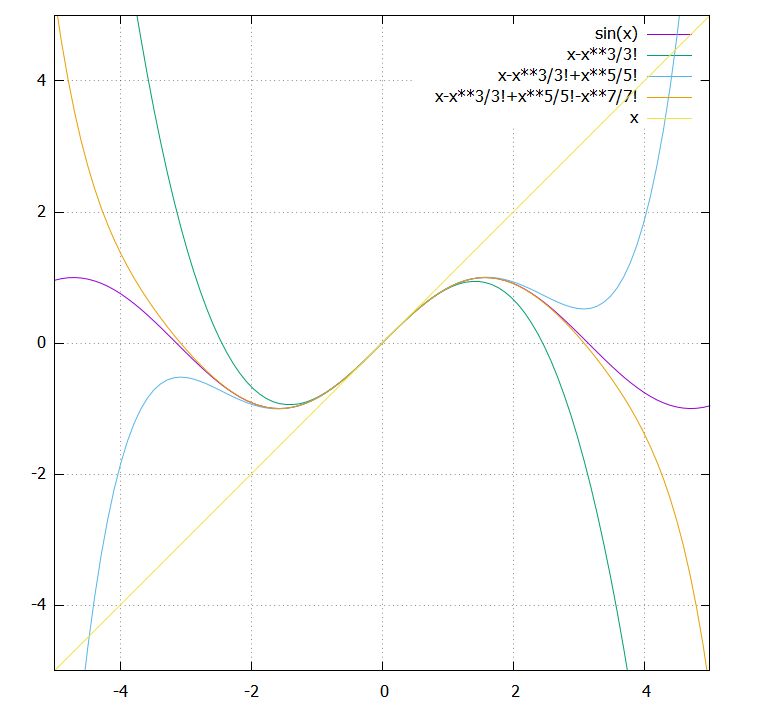
コラム テーラー展開（難易度1） 多くの関数f (x)は、abxcx 2 dx 3 ex 4 のような級数の形に展開することができます。 (この級数が収束する範囲内で) 例えば三角関数 sin x は のような無限級数となり、これはsin xのテーラー展開と呼ばれます。 関数f (x 平方根の近似値の求め方を知りたい！ こんにちは！この記事をかいているKenだよ。血糖値は高いね。 平方根をみていると、 どれくらいの大きさなんだろうな・・？ って思うことあるよね。 ルート！ルート！ っていわれてもデカさわからんし。
ルート 展開 近似
ルート 展開 近似-マクローリン展開の近似式への利用 マクローリン展開によって, ある関数はその導関数と \( x \) のベキ乗によって表すことができることを学んだ ここでは, 物理でいうところの近似は数学でいえばマクローリン展開をどこまで計算するかに等しい ことを17/9/16 /5/18 場合の数 前回の記事では， 重複する場合の数を求める際には「重複度で割る」という重複組合せの考え方がとても便利であることを説明しました． この重複組合せの考え方を使うと， ( a b) n の展開公式である 二項定理を導くことができ
電卓はいかに計算しているのか ライブドアニュース
ルートを使って表すべきなのか それとも2乗になる数が見つかるまで頑張るべきなのか判断がつきにくいよね。 だから 大きい数の平方根を考えていくためには どの数は、ルートを使わなくても表せるのか ということを多少は、覚えておく必要があります。 2．テイラー展開 1のマクローリン展開の拡張バージョンがテイラー展開となります。 テイラー展開をすると、、関数 \( f(x) \) の\( x \fallingdotseq 0 \) だけでなく、様々な \( x \) のときの近似を考えることができるようになります（様々な \( x \) のまわりでの展開ができるようになりま 追記 @scivola さんのコメントより一部修正させて頂きました。修正箇所は下段コメントをご確認ください。 テイラー展開の応用 テイラー級数を応用し、平方根などの近似を求めよう 1 x のk乗のテイラー級数への展開
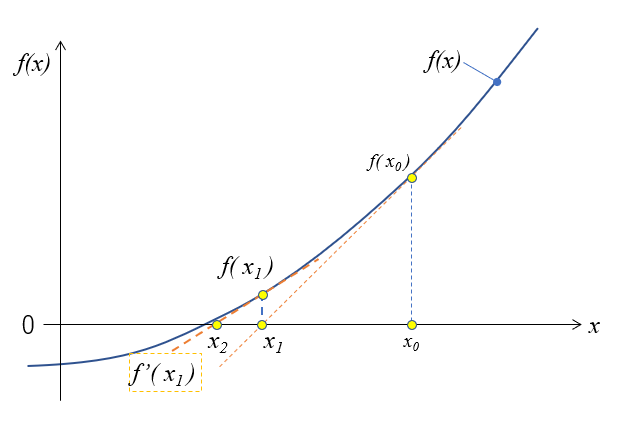
こんにちは！ほけきよです。 皆さん、πを知っていますか？？あの314以降無限に続く円周率です。 昔、どこかのお偉いさんが「314って中途半端じゃね？www3にしようぜ」 とかいって一時期円周率が3になりかけました。でもそれは円じゃなくて六角形だからだめです。近似式とマクローリン展開 一次関数（接線）で近似するのが一次近似です。より一般に， f (x) f(x) f (x) を n n n 次関数で近似するのが n n n 次近似です。当然ですが n n n が大きいほど精密な近似になりになる。1次の近似分数は1=4 で、1年に本当の日数は1=4 日多いというわけで、4年に1 度閏年を設けて、1日増やしておかないといけないことになる。 しかし、2次の近似分数は 1 41 7 = 7 29 日となり、100年の間に100× 7 =
ルート 展開 近似のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason | コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason | 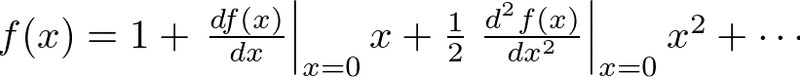 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
「ルート 展開 近似」の画像ギャラリー、詳細は各画像をクリックしてください。
 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason | 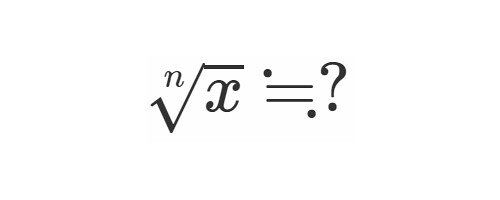 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
「ルート 展開 近似」の画像ギャラリー、詳細は各画像をクリックしてください。
コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |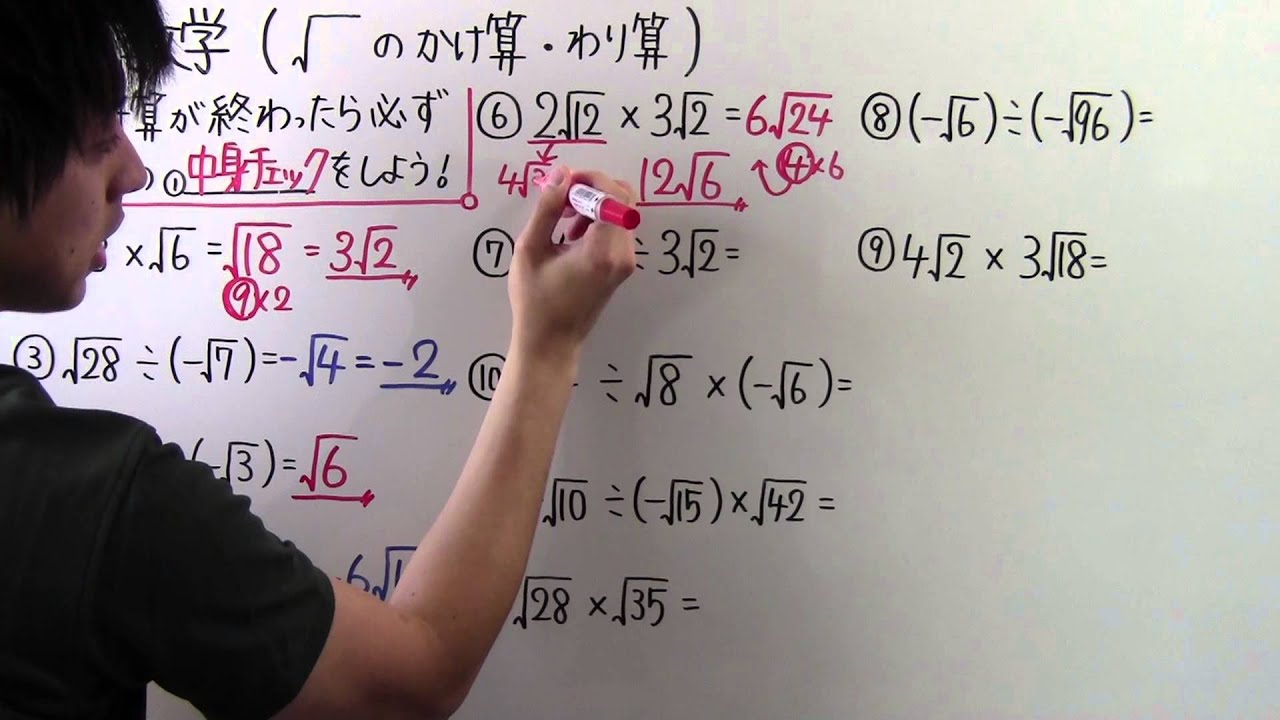
コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason | コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
「ルート 展開 近似」の画像ギャラリー、詳細は各画像をクリックしてください。
 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason | 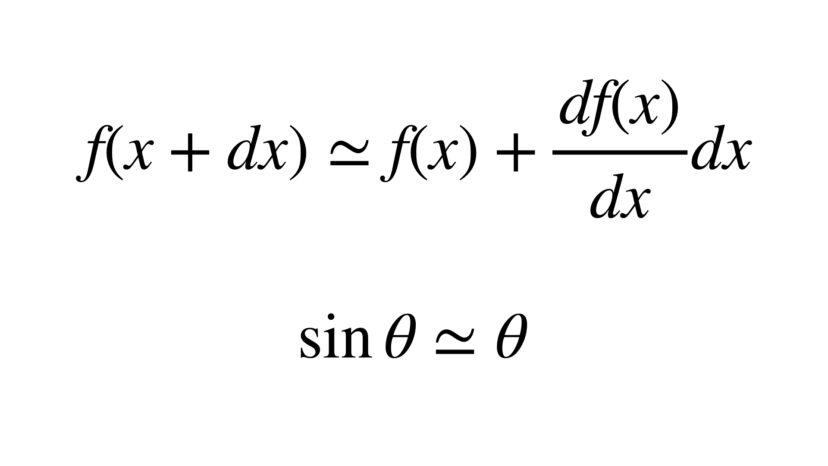 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
「ルート 展開 近似」の画像ギャラリー、詳細は各画像をクリックしてください。
 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason | コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
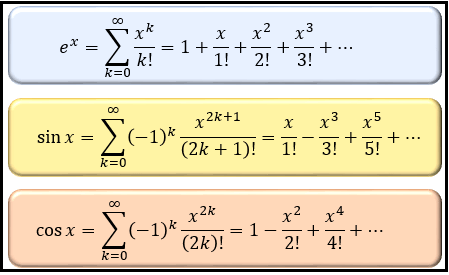 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason | コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
「ルート 展開 近似」の画像ギャラリー、詳細は各画像をクリックしてください。
 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason | コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason | コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason | コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
「ルート 展開 近似」の画像ギャラリー、詳細は各画像をクリックしてください。
 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason | 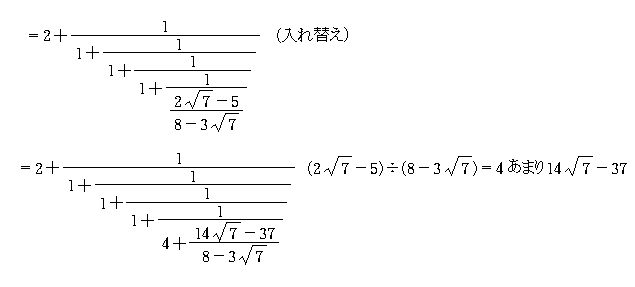 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
「ルート 展開 近似」の画像ギャラリー、詳細は各画像をクリックしてください。
 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason | コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason | 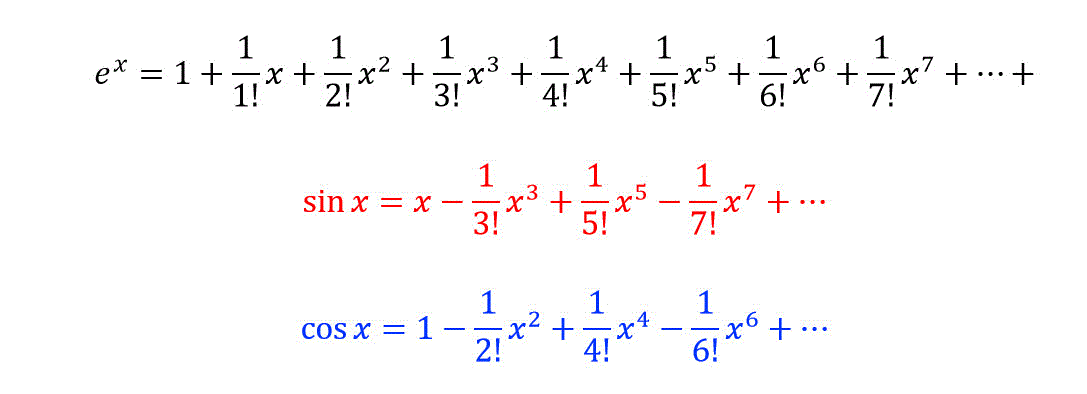 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
「ルート 展開 近似」の画像ギャラリー、詳細は各画像をクリックしてください。
コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason | コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
「ルート 展開 近似」の画像ギャラリー、詳細は各画像をクリックしてください。
 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason | 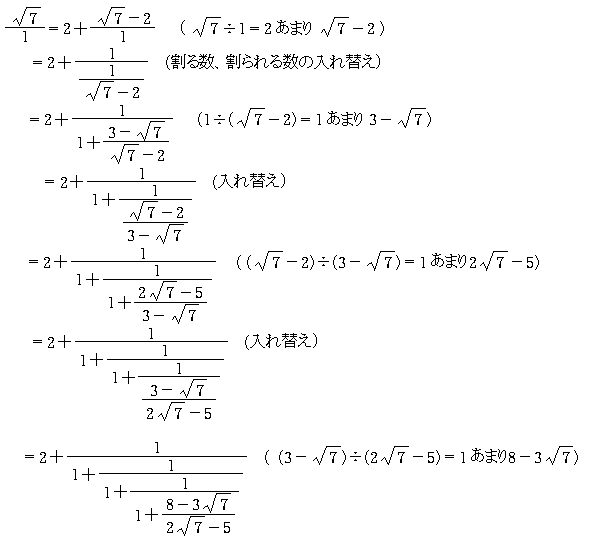 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
「ルート 展開 近似」の画像ギャラリー、詳細は各画像をクリックしてください。
 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
「ルート 展開 近似」の画像ギャラリー、詳細は各画像をクリックしてください。
 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
 コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |  コレクション ルート 展開 近似 ルート 展開 近似 Vantasiaseason |
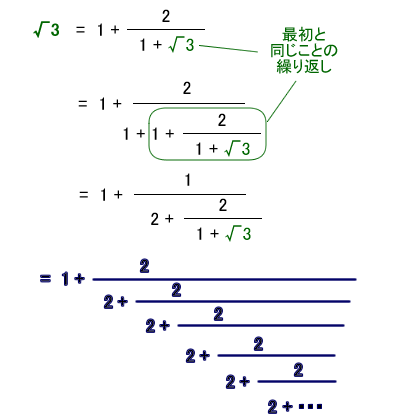
この は連分数展開してもてんで出鱈目。 比べると がいかに品行方正かがわかるだろう。 もう一つは、この連分数を途中まで計算すれば、それが の近似値になるということ。 つまり の近似値は簡単に計算できることがわかるだろう。 でも今日はここまで(^^) テイラー展開とは、関数 f ( x) を多項式で近似する手法です。 という条件下において、 f ( x) は以下のような無限級数で表すことができます。 この式のことを、 「 f ( x) の a を中心としたテイラー展開」 と言います。 テイラー展開は、 a = 0 の場合につい
Incoming Term: ルート 展開 近似,
0 件のコメント:
コメントを投稿